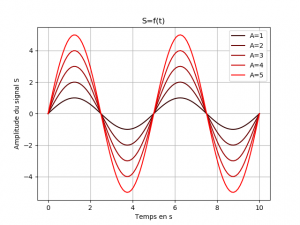
Représenter un signal périodique et illustrer l’influence de son amplitude sur sa représentation.
Pour illustrer l’influence de l’amplitude d’un signal périodique sur sa représentation, il est possible de tracer un réseau de courbes représentant le même signal mais dont l’amplitude varie.
Pour cela, le programme principal est organisé de la façon suivante :
-
- Une liste contient les valeurs des amplitudes successives de chaque courbe
A=[1,2,3,4,5], - Une liste contient la liste des couleurs de chacune des courbes
C=[(0.2,0,0),(0.4,0,0),(0.6,0,0),(0.8,0,0),(1,0,0)]. Les couleurs sont codés avec le système RVB. La proportion de chacune des couleurs est désignée par une valeur comprise entre 0 et 1. - La période du signal est fixée à 5 s.
- Un tableau Numpy contenant les valeurs du temps t est créé avec 100 valeurs variant de 0 à 10 :
t=np.linspace(0,10,100). - La boucle for s’exécute autant de fois qu’il y a de valeurs d’amplitudes dans la liste A. Elle créé un nouveau tableau Numpy nommé S en calculant
S = A[i]*np.sin((2*np.pi/T)*t). La chaîne de caractères « légende » qui s’affichera en légende sur la fenêtre graphique est crée de manière à indiquer les valeurs successives des amplitudes des différentes courbes tracées. Un appel à la fonctiontracer(t,S,legende,C[i])est réalisé avec quatre paramètres : le tableau t, le tableau S, la légende à afficher ainsi que la couleur de la courbe choisie dans la liste C. Cette fonction est chargée de tracer chacune des courbes.
- Une liste contient les valeurs des amplitudes successives de chaque courbe
import matplotlib.pyplot as plt
import numpy as np
#Les fonctions-----------------------------------------
def tracer(t,S,text,couleur):
plt.title("S=f(t)")
plt.xlabel("Temps en s")
plt.ylabel("Amplitude du signal S")
plt.grid()
plt.plot(t, S, color=couleur, label=text)
plt.legend()
#Le programme principal--------------------------------
A=[1,2,3,4,5]
C=[(0.2,0,0),(0.4,0,0),(0.6,0,0),(0.8,0,0),(1,0,0)]
T=5
t=np.linspace(0,10,100)
for i in range(len(A)):
S = A[i]*np.sin((2*np.pi/T)*t)
legende="A="+str(A[i])
tracer(t,S,legende,C[i])
plt.show()
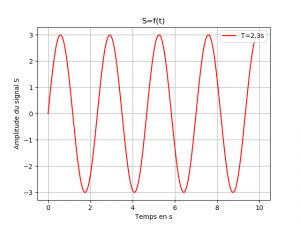
Représenter un signal périodique et illustrer l’influence de sa période sur sa représentation.
Pour montrer l’influence de la période du signal sur sa représentation, l’utilisation d’un réseau de courbe comme dans le programme précédent n’est pas la solution la plus pertinente car la représentation est peu lisible. Dans le programme proposé ci-dessous, des représentations du signal se succèdent avec une période de plus en plus grande. On obtient ainsi un effet d’animation qui montre l’influence de la période T sur la représentation du signal. Dans le programme principal :
-
- L’amplitude du signal est fixée à une valeur de 3,
- Un tableau Numpy contenant les valeurs de T est créé :
T=np.linspace(1,5,40). Ces 40 valeurs sont comprises entre 1 s et 5 s. - Une boucle for va, pour chaque valeur de période contenue dans le tableau T :
-
- Créer un tableau S contenant les valeurs de l’amplitude du signal au cours du temps,
- Créer la chaîne de caractère utilisée comme légende sur la représentation graphique en concaténant le texte « T= » avec la valeur de la période formatée avec un chiffre avant et après le séparateur décimal,
- Faire appel à la fonction
tracer(t,S,legende)qui prend trois paramètres : le tableau t, le tableau S et la légende à afficher.
-
La fonction tracer(t,S,legende) commence par effacer la fenêtre graphique puis définit le titre du graphique, les noms des axes, affiche la grille, affiche la courbe correspondant aux valeurs du signal en rouge, place la légende en haut et à gauche du graphique et fait une pause de 0,2 s.
Les différentes courbes sont ainsi tracées toutes les 0,2 s ce qui donne l’effet d’animation.
import matplotlib.pyplot as plt
import numpy as np
#Les fonctions-----------------------------------------
def tracer(t,S,text):
plt.clf()
plt.title("S=f(t)")
plt.xlabel("Temps en s")
plt.ylabel("Amplitude du signal S")
plt.grid()
plt.plot(t, S, color='red', label=text)
plt.legend(loc='upper right')
plt.pause(0.2)
#Le programme principal--------------------------------
A=3
T=np.linspace(1,5,40)
t=np.linspace(0,10,500)
for i in range(len(T)):
S = A*np.sin((2*np.pi/T[i])*t)
legende="T={0:1.1f}s".format(T[i])
tracer(t,S,legende)
plt.show()
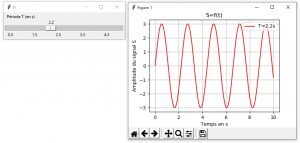
Il est également possible de travailler à l’aide du module Tkinter pour créer un curseur permettant de régler la valeur de T. La représentation graphique de l’onde est modifiée dès que la position du curseur est modifiée.
from tkinter import *
import matplotlib.pyplot as plt
import numpy as np
#Les fonctions--------------------------------------------
def afficher(val):
T=float(val)
A=3
t=np.linspace(0,10,500)
S = A*np.sin((2*np.pi/T)*t)
legende="T={0:1.1f}s".format(T)
plt.clf()
plt.title("S=f(t)")
plt.xlabel("Temps en s")
plt.ylabel("Amplitude du signal S")
plt.grid()
plt.plot(t, S, color='red', label=legende)
plt.legend(loc='upper right')
#Le programme principal-----------------------------------
Interface=Tk()
plt.ion()
T=Scale(Interface, orient='horizontal', from_=0.5, to=5,
resolution=0.1, tickinterval=1, length=350,
label='Période T (en s)', command=afficher)
T.pack()
Interface.mainloop()
L’étude du programme principal nous montre une nouvelle manière de coder. Nous sommes ici dans une programmation davantage orientée objet. L’objet Interface est créé dans la première ligne du programme principal. Le graphique matplotlib.pyplot est paramétré en mode interactif. Un widget de type Scale (curseur) est créé. Son objet parent est l’interface. Le curseur est placé horizontalement, il est gradué de 0,5 à 5 s avec un pas de 0,1 s. Des graduations sont séparées d’un seconde. La longueur du curseur est fixée à 350 pixels. On lui associe un texte (label). Dès que la position du curseur est changée par l’utilisateur, la fonction afficher est appelée.
Le widget scale nommé T est placé sur l’interface T.pack(). L’inspecteur d’événement est démarré : Interface.mainloop(). Il surveille toutes les actions de l’utilisateur (modification de la position du curseur, fermeture de l’interface).
Dans la fonction afficher, la valeur du curseur (val) est convertie en un nombre flottant et est associée à la valeur de la période T. Les tableaux Numpy t et S sont créés. La légende est mise en forme. Le graphique précédent est effacé et le nouveau est tracé. La légende est placée en haut et à droite de la représentation graphique. Lorsque le programme s’exécute, l’interface ainsi que la fenêtre graphique sont affichées :
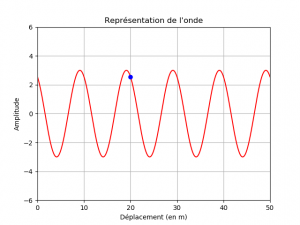
Simuler la propagation d’une onde périodique.
Pour simuler le déplacement d’une onde, il est possible de commencer par fixer l’amplitude A de l’onde, sa période T ainsi que sa célérité v comme le propose le programme ci-dessous. On fait ensuite le choix de calculer 5 fois la valeur de la longueur d’onde et de stocker cette valeur dans la variable x_max qui servira à afficher 5 longueurs d’onde du signal dans la fenêtre graphique.
Un tableau Numpy est créé : t=np.linspace(0,10,100). Il est constitué de 100 valeurs du temps réparties sur l’intervalle compris entre 0 et 10 s. Un second tableau Numpy est construit : x=np.linspace(0,x_max,100*x_max). Il contient 100*x_max valeurs d’abscisse réparties sur l’intervalle compris entre 0 et x_max.
Une boucle calcule ensuite pour chaque valeur du temps la valeur de l’amplitude de l’onde notée y et fait ensuite appel à la fonction tracer(x,y,A,x_max) avec quatre paramètres. Cette fonction commence par effacer la représentation précédente puis elle définit un certain nombre d’éléments de la représentation graphique : son titre, le nom de chacun des axes ainsi que leurs limites, affiche la grille puis trace l’onde sinusoïdale en rouge. Une courte pause est effectuée. A chaque itération de la boucle, le graphique est effacer et retracer pour montrer le déplacement de l’onde.
import matplotlib.pyplot as plt
import numpy as np
#Les fonctions-----------------------------------------
def tracer(x, y, amplitude,x_max):
plt.clf()
plt.title("Représentation de l'onde")
plt.xlabel("Déplacement (en m)")
plt.xlim(0,x_max)
plt.ylabel("Amplitude")
plt.ylim(-2*amplitude,2*amplitude)
plt.grid()
plt.plot(x, y, color='red')
plt.pause(0.01)
#Le programme principal--------------------------------
A=3
T=2
v=5
x_max=50
t=np.linspace(0,10,100)
x=np.linspace(0,x_max,100*x_max)
for i in range(len(t)):
y = A*np.sin((2*np.pi/T)*(t[i]-x/v))
tracer(x,y,A,x_max)
plt.show()
Pour travailler sur les notions de périodicité spatiale et temporelle, il peut être intéressant d’ajouter un point d’abscisse fixe sur la représentation graphique. Le programme ci-dessus est modifié de manière à répondre à cet objectif :
import matplotlib.pyplot as plt
import numpy as np
#Les fonctions-----------------------------------------
def tracer(x, y, amplitude, x_max, x_point, y_point):
plt.clf()
plt.title("Représentation de l'onde")
plt.xlabel("Déplacement (en m)")
plt.xlim(0,x_max)
plt.ylabel("Amplitude")
plt.ylim(-2*amplitude,2*amplitude)
plt.grid()
plt.plot(x, y, color='red')
plt.plot(x_point,y_point,'bo')
plt.pause(0.01)
#Le programme principal--------------------------------
A=3
T=2
v=5
x_max=50
xP=20
t=np.linspace(0,10,100)
x=np.linspace(0,x_max,100*x_max)
for i in range(len(t)):
y = A*np.sin((2*np.pi/T)*(t[i]-x/v))
yP = A*np.sin((2*np.pi/T)*(t[i]-xP/v))
tracer(x,y,A,x_max,xP,yP)
plt.show()