Déterminer l’état final d’un système chimique siège d’une transformation chimique totale.
Dans cet article, la transformation chimique s’écrit :
a A + b B → …….
Au départ du programme, plusieurs demandes à l’utilisateur peuvent être réalisées :
- le nombre stœchiométrique a,
- la quantité de matière initiale en réactif A,
- le nombre stœchiométrique b,
- la quantité de matière initiale en réactif B.
Les informations saisies grâce à la commande input sont des chaines de caractères. Or, il est nécessaire de les transtypere en nombres flottants de manière à pouvoir effectuer des calculs sur les valeurs saisies (float).
Ces informations sont envoyées à la fonction avancement_maximal(a,n_Ai,b,n_Bi). Elle calcule et renvoie au programme principal la valeur de l’avancement maximal de la transformation chimique. Dans le programme principal, cette valeur est rangée dans la variable x_max : x_max=avancement_maximal(a,n_Ai,b,n_Bi).
Ensuite, les informations saisies, ainsi que la valeur de l’avancement maximal, sont envoyés à la fonction etat_final(a,n_Ai,b,n_Bi,x_max). Cette fonction commence par calculer les quantités n_A et n_B d’espèce A et B à l’état final de la transformation. Ensuite, trois situations sont possibles :
- Ces deux quantités sont nulles, nous sommes alors dans les conditions stœchiométriques,
- La quantité de l’espèce A est nulle. A est le réactif limitant et la fonction affiche la valeur de x_max formatée en notation scientifique avec deux chiffres après la virgule. Elle calcule puis affiche la quantité restante de l’espèce B avec le même formatage.
- Si la quantité de A n’est pas nulle, c’est l’espèce B qui est le réactif limitant. La fonction affiche la valeur de x_max formatée en notation scientifique avec deux chiffres après la virgule. Elle calcule puis affiche la quantité restante de l’espèce A avec le même formatage.
Remarque 1 : la nullité des valeurs de n_A et n_B n’est pas vérifiée avec le test if n_A==0 : en raison des incertitudes sur le codage des nombres flottants. Le test consiste à vérifier laquelle des valeurs entre n_A et n_B est très proche de 0 : elif n_A<1E-10 :.
Remarque 2 : le formatage des données affichées est réalisé à l’aide de la fonction « format ». Dans la ligne print("x_max = {0:1.2E} mol.".format(x_max)), la valeur de la variable x_max est insérée à l’endroit où apparait {0:1.2E}. Dans le code {0:1.2E}:
-
- La valeur 0 donne l’index de la variable à afficher parmi celles contenue dans la commande
format(x_max). Ici, la variable x_max a un index égal à 0. La commande « format » peut contenir plusieurs variables qui peuvent être affichées dans une même phrase à l’écran. Si une seconde variable était présente, son index serait égal à 1. - La valeur 1 précise le nombre de chiffres que l’on veut inscrire avant le séparateur décimal,
- La valeur 2 indique le nombre de chiffres que l’on veut afficher après le séparateur décimal,
- « E » indique que l’on souhaite utiliser une notation par exposant utilisant le symbole ‘E’
- La valeur 0 donne l’index de la variable à afficher parmi celles contenue dans la commande
#Les fonctions------------------------------------------------------
def avancement_maximal(a,n_Ai,b,n_Bi):
x_max=min(n_Ai/a, n_Bi/b)
return x_max
def etat_final(a,n_Ai,b,n_Bi,x_max):
n_A=n_Ai-a*x_max
n_B=n_Bi-b*x_max
if (n_A<1E-10 and n_B<1E-10):
print("Nous sommes dans les conditions stoechiométriques")
print("x_max = {0:1.2E} mol.".format(x_max))
elif n_A<1E-10 :
n_A=0
print("A est le réactif limitant.")
print("x_max = {0:1.2E} mol.".format(x_max))
print("A la fin de la transformation, il n'y a plus de A.")
print("Il reste {0:1.2E} mol de B.".format(n_B))
else :
n_B=0
print("B est le réactif limitant.")
print("x_max = {0:1.2E} mol.".format(x_max))
print("A la fin de la transformation, il n'y a plus de B.")
print("Il reste {0:1.2E} mol de A.".format(n_A))
#Le programme principal---------------------------------------------
#Equation du type aA + bB -> ........
a=float(input("Entrez le nombre stoechiométrique a :"))
n_Ai=float(input("n_Ai = "))
b=float(input("Entrez le nombre stoechiométrique b :"))
n_Bi=float(input("n_Bi = "))
x_max=avancement_maximal(a,n_Ai,b,n_Bi)
etat_final(a,n_Ai,b,n_Bi,x_max)
Le programme est testé avec les valeurs suivantes : a=1, n_Ai=2 mol, b=2, n_Bi=3mol affiche :
>>> B est le réactif limitant. x_max = 1.50E+00 mol. A la fin de la transformation, il n'y a plus de B. Il reste 5.00E-01 mol de A.
Il est possible de faire le choix d’alléger le code de ce programme en n’ayant pas recours à des demandes à l’utilisateur. Le programme principal est alors nettement simplifié :
#Le programme principal--------------------------------------------- #Equation du type aA + bB -> ........ a, b = 1, 2 n_Ai, n_Bi= 1E-2, 4E-2 x_max=avancement_maximal(a,n_Ai,b,n_Bi) etat_final(a,n_Ai,b,n_Bi,x_max)
Modélisation de l’évolution des quantités de matières d’un système chimique siège d’une transformation chimique totale.
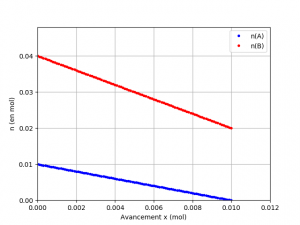
Le module matplotlib.pyplot permet de tracer des graphiques dynamiques. L’activation du graphique s’effectue avec la commande plt.ion(). Son arrêt en fin de programme s’effectue avec plt.ioff(). Dans le programme principal, l’utilisateur saisi les nombres stœchiométriques des réactifs ainsi que leurs quantités de matière initiales. Le programme appel ensuite la fonction courbes(a,n_Ai,b,n_Bi). Après l’exécution complète de cette fonction, le graphique dynamique est désactivé mais la fenêtre graphique reste affichée pour permettre une exploitation par l’utilisateur.
La fonction courbes(a,n_Ai,b,n_Bi) commence par quelques instructions d’initialisation de variables :
-
- L’avancement x est mis à 0,
- La quantité d’espèce A est initialisée à l’aide de la valeur transmise en paramètre de la fonction. Il en est de même pour la quantité d’espèce B,
- Le pas de variation de l’avancement, nécessaire pour les calculs, est initialisé au centième de la petite des deux quantités de matière,
- L’avancement maximal est calculé dans la variable x_max,
- Cette valeur va âtre utile pour fixer la limite de l’axe des abscisses à 1.2 fois cette valeur,
- La limite de l’axe des ordonnées est fixée à 1,2 fois la plus grande quantité de matière initiale,
- Les noms des axes ainsi que la grille sont affichés,
- Les lignes 17, 18 et 19 placent les premiers points de chacune des courbes ainsi que la légende dont l’affichage utilise les « label » des point placés,
- La boucle de la ligne 20 permet au programme d’incrémenter la valeur de l’avancement x de la quantité dx, de calculer les quantités respectives de A et de B et de placer les points correspondant sur le graphique tant que les deux quantités de matière sont strictement positives. Dès que l’un des réactifs est épuisé, le tracé du graphique s’arrête.
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def courbes(a,n_Ai,b,n_Bi):
x=0
n_A=n_Ai
n_B=n_Bi
dx=(min(n_A,n_B)/100)
plt.ion()
x_max=min(n_Ai/a,n_Bi/b)
plt.xlim(0,1.2*x_max)
plt.ylim(0,1.2*max(n_A,n_B))
plt.xlabel('Avancement x (mol)')
plt.ylabel('n (en mol)')
plt.grid()
plt.plot(x,n_A,'b.',label='n(A)')
plt.plot(x,n_B,'r.',label='n(B)')
plt.legend()
while (n_A>0) and (n_B>0):
plt.plot(x,n_A,'b.')
plt.plot(x,n_B,'r.')
plt.pause(0.01)
x=x+dx
n_A=n_Ai-a*x
n_B=n_Bi-b*x
#Le programme principal---------------------------------------------
#Equation du type aA + bB -> ........
a, b = 1, 2
n_Ai, n_Bi= 1E-2, 4E-2
courbes(a,n_Ai,b,n_Bi)
plt.ioff()
plt.show()
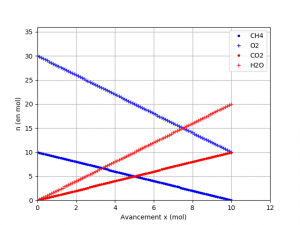
Le programme peut être développé pour permettre l’affichage de l’évolution des quantités des produits de la réaction :
a A + b B → c C + d D
Dans le programme principal, l’utilisateur saisi :
-
- Les nombres stœchiométriques a, b, c et d de l’équation,
- Les quantités initiales n_Ai, n_Bi, n_Ci, et n_Di de réactifs et de produits,
- Les noms des espèces chimiques A, B, C et D.
Les quantités des deux réactifs sont affichées en bleu alors les quantités des deux produits apparaissent en rouge sur le graphique.
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def courbes(a,b,c,d,n_Ai,n_Bi,n_Ci,n_Di,A,B,C,D):
x=0
n_A, n_B, n_C, n_D = n_Ai, n_Bi, n_Ci, n_Di
dx=(min(n_A,n_B)/100)
plt.ion()
x_max=min(n_Ai/a,n_Bi/b)
plt.xlim(0,1.2*x_max)
plt.ylim(0,1.2*max(n_A,n_B))
plt.xlabel('Avancement x (mol)')
plt.ylabel('n (en mol)')
plt.grid()
plt.plot(x,n_A,'b.',label=A)
plt.plot(x,n_B,'b+',label=B)
plt.plot(x,n_C,'r.',label=C)
plt.plot(x,n_D,'r+',label=D)
plt.legend()
while (n_A>0) and (n_B>0):
plt.plot(x,n_A,'b.')
plt.plot(x,n_B,'b+')
plt.plot(x,n_C,'r.')
plt.plot(x,n_D,'r+')
plt.pause(0.01)
x=x+dx
n_A=n_Ai-a*x
n_B=n_Bi-b*x
n_C=n_Ci+c*x
n_D=n_Di+d*x
#Le programme principal---------------------------------------------
#Equation du type aA + bB -> cC + dD
a, b, c, d = 1, 2, 1, 2
n_Ai, n_Bi, n_Ci, n_Di= 10, 30, 0, 0
A, B, C, D = "CH4", "O2", "CO2", "H2O"
courbes(a,b,c,d,n_Ai,n_Bi,n_Ci,n_Di,A,B,C,D)
plt.ioff()
plt.show()