Effectuer le bilan énergétique d’un système en mouvement.
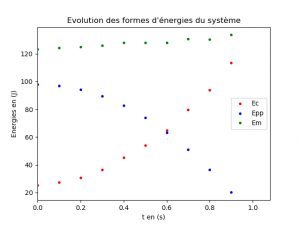
Il est possible de représenter l’évolution des différentes formes d’énergie du système en mouvement au cours du temps à l’aide du programme ci-dessous :
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def graphique(Ec, Epp, Em, t):
plt.title("Evolution des formes d'énergies du système")
plt.xlabel('t en (s)')
plt.ylabel('Energies en (J)')
plt.xlim(0,1.2*max(t))
plt.ylim=(0,1.2*max(Em))
plt.plot(t,Ec,'r.',label='Ec')
plt.plot(t,Epp,'b.',label='Epp')
plt.plot(t,Em,'g.',label='Em')
plt.legend()
def calcul_vitesses(abscisses,ordonnees,temps):
v=[]
for n in range(len(abscisses)-1):
v_x=(abscisses[n+1]-abscisses[n])/(temps[n+1]-temps[n])
v_y=(ordonnees[n+1]-ordonnees[n])/(temps[n+1]-temps[n])
v.append((v_x**2+v_y**2)**0.5)
temps=temps[:-1]
return v,temps
#Le programme principal--------------------------------------------
x=[0.00,0.50,1.00,1.50,2.00,2.50,3.00,3.50,4.00,4.50,5.00]
z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09]
t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00]
masse = 2
g=9.8
v, temps_v = calcul_vitesses(x,z,t)
#-----------------------------------
Ec=[0.5*masse*vitesse**2 for vitesse in v]
#-----------------------------------
Epp=[]
for i in range(len(v)):
Epp.append(masse*g*z[i])
#-----------------------------------
Em=[]
for i in range(len(v)):
Em.append(Ec[i]+Epp[i])
#-----------------------------------
graphique(Ec, Epp, Em, temps_v)
plt.show()
Dans le programme principal :
-
- Les listes contenant les coordonnées x et z du système sont saisies ainsi que la liste donnant les dates correspondant aux positions relevées du système,
- Deux constantes sont définies : la masse m du système et de l’intensité g de la pesanteur,
- Un appel à la fonction
calcul_vitesses(x,z,t)est effectué. Elle renvoie une liste contenant les valeurs de la vitesse du système dans ses différentes positions (sauf la dernière) ainsi que la liste des dates raccourcie d’une valeur pour que les dates correspondent aux valeurs des vitesses et que ces deux listes aient la même longueur. - La ligne 34 permet de remplir une liste nommée Ec avec les valeurs de l’énergie cinétique du système.
- Le code :
Epp=[] for i in range(len(v)): Epp.append(masse*g*z[i])permet de calculer l’énergie potentielle de pesanteur du système en obtenant une liste de même longueur que pour l’énergie cinétique (len(v)).
- La boucle suivante permet de calculer les valeurs de l’énergie mécanique du système.
- Un appel à la fonction
graphique(Ec, Epp, Em, temps_v)est ensuite réalisé. Cette fonction met en place tous les éléments du graphique que l’on souhaite obtenir : son titre, le nom des axes, les limites des axes, les trois courbes Ec=f(t), Epp=f(t) et Em=f(t) avec des couleurs différentes et une légende pour pouvoir se repérer. - Le graphique est enfin affiché.