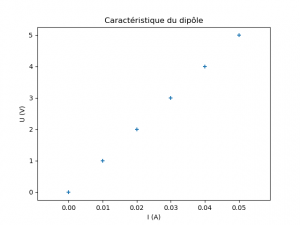
2nde : Signaux et capteurs avec Python.

Représenter un nuage de points associé à la caractéristique d’un dipôle.

Pour représenter un nuage de points, il est possible d’utiliser le module matplotlib.pyplot. Le graphique de type “scatter” permet une représentation de données en nuage de points.

Une étude expérimentale permet d’avoir deux listes : l’une contenant les valeurs de la tension U aux bornes du dipôle et l’autre les valeurs de l’intensité I du courant le traversant. Il est assez simple de construire une fonction courbe(x,y)qui prendra deux listes en argument pour mettre en forme la caractéristique du dipôle.

import matplotlib.pyplot as plt

#Les fonctions---------------------------------------------

def courbe(x,y):
    plt.xlabel("I (A)")
    plt.ylabel("U (V)")
    plt.title("Caractéristique du dipôle")
    plt.scatter(x,y,marker='+')

#Le programme principal------------------------------------

U=[0,1,2,3,4,5]
I=[0,0.01,0.02,0.03,0.04,0.05]

courbe(I,U)
plt.show()

Modéliser la caractéristique du dipôle.

Pour modéliser la caractéristique, il est possible d’utiliser un autre module de Python : Numpy. Le module sera importé avec un nom court (alias) “np”. La fonction polyfit de Numpy demande trois arguments : la liste des abscisses, la liste des ordonnées et le degré du polynôme choisi pour le modèle. Pour des raisons pratiques, il est intéressant que les listes U et I soient déclarées comme des tableaux numpy, des “numpy array”.

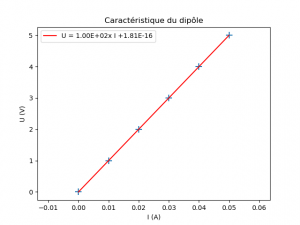
Pour un polynôme de degré 1, la fonction polyfit renvoie un tableau numpy contenant deux valeurs : [1.00000000e+02 1.81298661e-16] (pour l’exemple traité ici). Les valeurs de ce tableau correspondent aux coefficients du polynôme modèle. La première valeur correspond au coefficient du terme de degré le plus élevé. Pour une droite, la première valeur correspond donc à son coefficient directeur et le second à son ordonnée à l’origine. La ligne modele=np.polyfit(I,U,1) range donc le tableau de résultat dans la variable nommée “modele” : modele = [1.00000000e+02 1.81298661e-16] . Pour accéder au coefficient directeur de la droite, il faut accéder à l’élément 0 du tableau “modele” soit modele[0]. L’accès à la valeur de l’ordonnée à l’origine s’effectue grâce à la syntaxe modele[1]. Il est alors possible d’écrire une fonction modelisation(x,y) prenant deux paramètres : le tableau contenant les valeurs des abscisses et celui contenant les valeurs des ordonnées :

def modelisation(x,y):
    modele=np.polyfit(x,y,1)
    equation=("U = "+format(modele[0],".2E")+"x I +"+format(modele[1],".2E"))
    plt.plot(x,modele[0]*x+modele[1],color='red',label=equation)
    plt.legend()

La ligne 3 de cette fonction met en forme l’équation de la droite qui sera affichée sur le graphique sous forme d’une légende. Les valeurs du coefficient directeur et de l’ordonnée à l’origine sont formatées en notation scientifique avec deux chiffres après la virgule : format(modele[0],".2E").

La ligne 4 permet de tracer une courbe prenant les valeurs de I en abscisse, calculant la valeur des ordonnées à partir du résultats de la modélisation et l’affichant en rouge sur le graphique avec son équation comme étiquette de légende.

Cette nouvelle fonction complète le programme affichant le nuage de point. Le modèle vient alors se superposer aux points de mesure :

import matplotlib.pyplot as plt
import numpy as np

#Les fonctions---------------------------------------------

def courbe(x,y):
    plt.xlabel("I (A)")
    plt.ylabel("U (V)")
    plt.title("Caractéristique du dipôle")
    plt.scatter(x,y,marker='+',s=100)

def modelisation(x,y):
    modele=np.polyfit(x,y,1)
    equation=("U = "+format(modele[0],".2E")+"x I +"+format(modele[1],".2E"))
    plt.plot(x,modele[0]*x+modele[1],color='red',label=equation)
    plt.legend()

#Le programme principal------------------------------------

U=np.array([0,1,2,3,4,5])
I=np.array([0,0.01,0.02,0.03,0.04,0.05])

courbe(I,U)
modelisation(I,U)
plt.show()

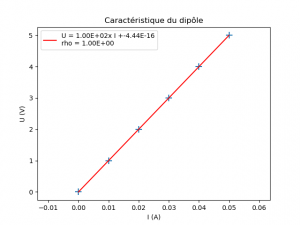
Pour modéliser la courbe, il est également possible d’utiliser le module scipy.stats qui fournit une fonction permettant de faire une régression linéaire : linregress. Cette fonction est importée en début de programme. La fonction modelisation(x,y) est donc modifiée pour s’adapter à cette fonction :

def modelisation(x,y):
    modele=linregress(x,y)
    equation=("U = "+format(modele[0],".2E")+"x I +"+format(modele[1],".2E")
    +"\n"+"rho = "+format(modele[2],".2E"))
    plt.plot(x,modele[0]*x+modele[1],color='red',label=equation)
    plt.legend()

La fonction linregress renvoi un tuple contenant cinq valeurs dont les trois premières peuvent être intéressantes :

Le coefficient directeur de la droite modèle,
Son ordonnée à l’origine,
Le coefficient de corrélation ρ.

La ligne 4 ajoute à l’équation de la droite la valeur du coefficient de corrélation après un retour à la ligne “\n”.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import linregress

#Les fonctions---------------------------------------------

def courbe(x,y):
    plt.xlabel("I (A)")
    plt.ylabel("U (V)")
    plt.title("Caractéristique du dipôle")
    plt.scatter(x,y,marker='+',s=100)

def modelisation(x,y):
    modele=linregress(x,y)
    equation=("U = "+format(modele[0],".2E")+"x I +"+format(modele[1],".2E")
    +"\n"+"rho = "+format(modele[2],".2E"))
    plt.plot(x,modele[0]*x+modele[1],color='red',label=equation)
    plt.legend()

#Le programme principal------------------------------------

U=np.array([0,1,2,3,4,5])
I=np.array([0,0.01,0.02,0.03,0.04,0.05])

courbe(I,U)
modelisation(I,U)
plt.show()

Il est également possible de développer une interface permettant aux élèves de réaliser une application permettant de modéliser la caractéristique du dipôle à l’aide d’un modèle personnel par la saisie d’un coefficient directeur et d’une ordonnée à l’origine. Il est également possible d’ajouter un bouton permettant de tracer le modèle calculé par Numpy.

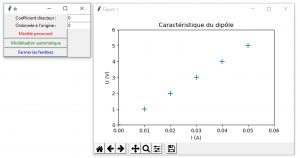
Ce programme exploite la bibliothèque Tkinter. L’interface est crée à la ligne 36. Le module pyplot est réglé en mode dynamique plt.ion(). Tous les éléments de l’interface sont créés et placés sur l’interface entre les lignes 41 et 62 :

- 2 étiquettes : Label permettant d’identifier les deux champs d’entrée,
- 2 champs d’entrée utilisateur : Entry,
- 3 boutons permettant d’exécuter :
  - - - la fonction modelisation(I,U) pour le bouton Modèle personnel,
      - la fonction modelisation_automatique(I,U) pour le bouton Modélisation automatique,
      - la fonction fermeture pour le bouton Fermer des fenêtres.

Tous les éléments de l’interface sont disposés sur une grille de 4 lignes et 2 colonnes grâce aux paramètres row et column de la méthode grid.

Après la construction de l’interface, la fonction courbe(I,U) est appelée pour tracer le graphique U=f(I). Pour finir, la boucle principale Interface.mainloop() est lancée (l’inspecteur d’événements qui surveille en permanence les actions de l’utilisateur sur l’interface).

from tkinter import *
import matplotlib.pyplot as plt
import numpy as np

#Les fonctions--------------------------------------------

def courbe(x,y):
    plt.clf()
    plt.xlabel("I (A)")
    plt.xlim(0,1.2*max(x))
    plt.ylabel("U (V)")
    plt.ylim(0,1.2*max(y))
    plt.title("Caractéristique du dipôle")
    plt.scatter(I,U,marker='+',s=100)

def modelisation(x,y):
    courbe(x,y)
    m=eval(a.get())
    p=eval(b.get())
    equation=("U = "+format(m,".2E")+"x I +"+format(p,".2E"))
    plt.plot(x,m*x+p,color='red',label=equation)
    plt.legend()

def modelisation_automatique(x,y):
    modele=np.polyfit(x,y,1)
    equation=("U = "+format(modele[0],".2E")+"x I +"+format(modele[1],".2E"))
    plt.plot(I,modele[0]*I+modele[1],color='green',label=equation)
    plt.legend()

def fermeture():
    plt.close()
    Interface.destroy()

#Le programme principal-----------------------------------

Interface=Tk()
plt.ion()
U=np.array([0,1,2,3,4,5])
I=np.array([0,0.01,0.02,0.03,0.04,0.05])

text_a=Label(Interface, text='Coefficient directeur :')
text_a.grid(row=0,column=0)
a=Entry(Interface, width=10)
a.grid(row=0,column=1)
a.insert(0,"0")
text_b=Label(Interface, text='Ordonnée à l\'origine :')
text_b.grid(row=1,column=0)
b=Entry(Interface, width=10)
b.grid(row=1,column=1)
b.insert(0,"0")
bouton=Button(Interface, text='Modèle personnel', width=24,
                foreground='red',
                command=lambda:modelisation(I,U))
bouton.grid(row=2,column=0)
bouton_mod_auto=Button(Interface, text='Modélisation automatique', width=24,
                        foreground='green',
                        command=lambda:modelisation_automatique(I,U))
bouton_mod_auto.grid(row=3,column=0)
bouton_fermer=Button(Interface, text='Fermer les fenêtres', width=24,
                        foreground='blue',
                        command=fermeture)
bouton_fermer.grid(row=4,column=0)

courbe(I,U)
Interface.mainloop()

2nde : Signaux et capteurs avec Python.

Représenter un nuage de points associé à la caractéristique d’un dipôle.

Modéliser la caractéristique du dipôle.

Cycle 4

Lycée

Liens utiles