Représenter les positions successives d’un système modélisé par un point lors d’une évolution unidimensionnelle ou bidimensionnelle.
Supposons que les coordonnées d’un système au cours du temps sont connues. Elle sont contenues dans deux listes : x et z.
Tracer un graphique dans python nécessite d’importer un module : import matplotlib.pyplot as plt
Ensuite, les deux listes x et z ont saisies. Pour représenter les positions successives du système au cours du temps, il est possible de tracer un graphique de type « scatter » c’est à dire « point par point » sans que ces derniers ne soient reliés les uns aux autres. La commande plt.scatter(x,z)demande au moins deux arguments : la liste des valeurs à placer en abscisse ainsi que la liste des valeurs à placer en ordonnée.
Attention, la commande plt.show() est indispensable pour que la fenêtre graphique s’affiche lors de l’exécution du programme.
import matplotlib.pyplot as plt x=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00] z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09] plt.scatter(x,z) plt.show()
Ce programme simple permet d’obtenir la représentation suivante :
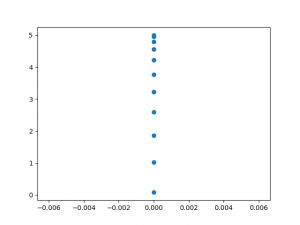
Il est intéressant d’améliorer cette représentation graphique en ajoutant un titre, le nom de la grandeur présente sur chacun des axes avec son unité et en remplaçant les points par des « plus » … Le nouveau code s’écrit :
import matplotlib.pyplot as plt
x=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00]
z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09]
plt.scatter(x,z,marker='+')
plt.title('Positions successives occupées par le système')
plt.xlabel('x en (m)')
plt.ylabel('Altitude z en (m)')
plt.show()
La représentation graphique obtenue est alors :
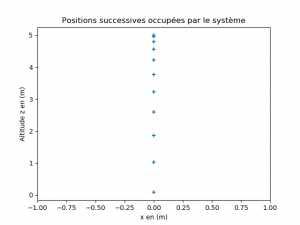
Ce programme peut être écrit sous forme d’une fonction réutilisable dans un programme plus complexe. La fonction tracer_des_positions() prend deux arguments lorsqu’elle est appelée depuis le programme principal (ligne 16) : la liste des abscisses et la liste des ordonnées.
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def tracer_des_positions(abscisses,ordonnees):
plt.scatter(abscisses,ordonnees,marker='+')
plt.title('Positions successives occupées par le système')
plt.xlabel('x en (m)')
plt.ylabel('Altitude z en (m)')
#Le programme principal--------------------------------------------
x=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00]
z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09]
tracer_des_positions(x,z)
plt.show()
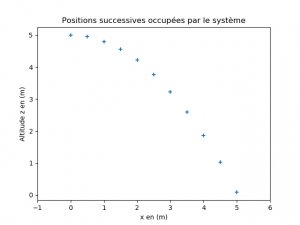
Dans le cas d’un mouvement bidimensionnel, seules les listes des positions changent. La fonction tracer_des_positions() reste identique. L’exemple suivant présente un mouvement dans le champ de pesanteur terrestre :
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def tracer_des_positions(abscisses,ordonnees):
plt.scatter(abscisses,ordonnees,marker='+')
plt.title('Positions successives occupées par le système')
plt.xlabel('x en (m)')
plt.ylabel('Altitude z en (m)')
#Le programme principal--------------------------------------------
x=[0.00,0.50,1.00,1.50,2.00,2.50,3.00,3.50,4.00,4.50,5.00]
z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09]
tracer_des_positions(x,z)
plt.show()
Représenter des vecteurs vitesse d’un système modélisé par un point lors d’un mouvement.
Plusieurs hypothèses de travail sont possibles. Soit les élèves disposent des valeurs de la vitesse du corps au cours de son mouvement, soit il est possible de les calculer en créant une fonction. Le travail s’effectuera sur un mouvement rectiligne. Considérons que la vitesse du corps n’est pas connue. Elle est calculée dans le programme ci-dessous grâce à la fonction calcul_vitesses(abscisses,temps) . Le mouvement étudié est à une dimension. La vitesse est calculée avec la méthode suivante : la vitesse au point n est calculée sur le déplacement du point n au point n+1. La fonction demande deux listes en paramètres : la liste des abscisses et la liste du temps. Elle retourne à son tour deux listes au programme principal : la liste des vitesses instantanées sauf pour le dernier point pour lequel le calcul n’est pas possible (il n’y a pas de point n+1 disponible). La liste du temps retournée temps_v contient les mêmes valeurs que la liste t mais la dernière valeur a été retirée à la ligne 9. L’appel à cette fonction qui s’effectue depuis le programme principal range les deux listes renvoyées par la fonction dans les listes v et temps_v à la ligne 17.
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def calcul_vitesses(abscisses,temps):
v=[]
for i in range(len(abscisses)-1):
v.append((abscisses[i+1]-abscisses[i])/(temps[i+1]-temps[i]))
temps=temps[:-1]
return v,temps
#Le programme principal--------------------------------------------
x=[0.00,0.01,0.04,0.09,0.16,0.25,0.36,0.49,0.64,0.81,1.00]
t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00]
v,temps_v=calcul_vitesses(x,t)
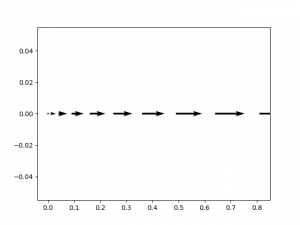
Pour représenter les vecteurs vitesse, nous allons faire appel à la fonction quiver du module matplotlib.pyplot. Elle permet de représenter un vecteur de coordonnées (U,V) au point de coordonnées (X,Y) avec la syntaxe plt.quiver(X, Y, U, V). Il est donc possible de créer une nouvelle fonction representation_vecteur_vitesse(abscisses,vitesses) qui prend deux listes en paramètres. La boucle présente dans cette fonction permet de parcourir la liste des abscisses, d’extraire la vitesse de chaque point de la liste des vitesses et de représenter le vecteur de coordonnées (vitesse[i], 0) en chaque point de coordonnées (abscisses[i],0). La longueur des vecteurs est calculée à partir de l’échelle des axes x et y avec un facteur de réduction de 15.
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def calcul_vitesses(abscisses,temps):
v=[]
for n in range(len(abscisses)-1):
v.append((abscisses[n+1]-abscisses[n])/(temps[n+1]-temps[n]))
temps=temps[:-1]
return v,temps
def representation_vecteur_vitesse(abscisses,vitesses):
for i in range(len(vitesses)):
plt.quiver(abscisses[i], 0 ,vitesses[i] , 0, scale_units='xy',angles='xy', scale=15)
#Le programme principal--------------------------------------------
x=[0.00,0.01,0.04,0.09,0.16,0.25,0.36,0.49,0.64,0.81,1.00]
t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00]
v,temps_v=calcul_vitesses(x,t)
representation_vecteur_vitesse(x,v)
plt.show()
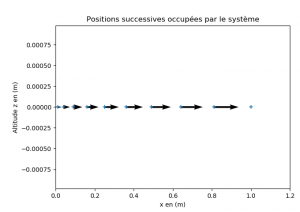
Il peut être intéressant de représenter également les positions successives occupées par le système au cours du temps en ajoutant dans le programme précédent, la fonction tracer_des_positions() écrite dans un programme précédent. Cela nécessite simplement d’ajouter la liste des altitudes z du système mais qui seront toutes nulles dans le cas de notre mouvement à une dimension. Dans le nouveau programme, c’est la fonction représentation_vecteur_vitesse() qui appellera la fonction tracer_des_positions() après la définition des vecteurs grâce à la fonction plt.quiver().
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def Tracer_des_positions(abscisses,ordonnees):
plt.scatter(abscisses,ordonnees,marker='+')
plt.title('Positions successives occupées par le système')
plt.xlabel('x en (m)')
plt.ylabel('Altitude z en (m)')
plt.xlim(0.8*min(abscisses),1.2*max(abscisses))
def calcul_vitesses(abscisses,temps):
v=[]
for n in range(len(abscisses)-1):
v.append((abscisses[n+1]-abscisses[n])/(temps[n+1]-temps[n]))
temps=temps[:-1]
return v,temps
def representation_vecteur_vitesse(abscisses,ordonnees,vitesses):
for i in range(len(vitesses)):
plt.quiver(abscisses[i], 0 ,vitesses[i] , 0, scale_units='xy',angles='xy', scale=15)
Tracer_des_positions(abscisses,ordonnees)
#Le programme principal--------------------------------------------
x=[0.00,0.01,0.04,0.09,0.16,0.25,0.36,0.49,0.64,0.81,1.00]
z=[0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00,0.00]
t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00]
v,temps_v=calcul_vitesses(x,t)
representation_vecteur_vitesse(x,z,v)
plt.show()
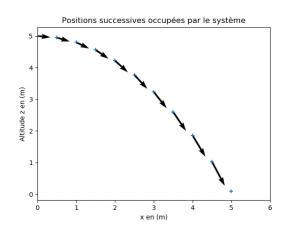
Avec un mouvement à deux dimensions, le programme peut s’écrire de la manière suivante :
import matplotlib.pyplot as plt
#Les fonctions------------------------------------------------------
def Tracer_des_positions(abscisses,ordonnees):
plt.scatter(abscisses,ordonnees,marker='+')
plt.title('Positions successives occupées par le système')
plt.xlabel('x en (m)')
plt.ylabel('Altitude z en (m)')
plt.xlim(0.8*min(abscisses),1.2*max(abscisses))
def calcul_vitesses(abscisses,ordonnees,temps):
v_x=[]
v_y=[]
for n in range(len(abscisses)-1):
print(n)
v_x.append((abscisses[n+1]-abscisses[n])/(temps[n+1]-temps[n]))
v_y.append((ordonnees[n+1]-ordonnees[n])/(temps[n+1]-temps[n]))
temps=temps[:-1]
return v_x,v_y,temps
def representation_vecteur_vitesse(abscisses,ordonnees,v_x,v_y):
for i in range(len(v_x)):
plt.quiver(abscisses[i], ordonnees[i] ,v_x[i] , v_y[i], scale_units='xy',angles='xy', scale=15)
Tracer_des_positions(abscisses,ordonnees)
#Le programme principal--------------------------------------------
x=[0.00,0.50,1.00,1.50,2.00,2.50,3.00,3.50,4.00,4.50,5.00]
z=[5.00,4.95,4.80,4.56,4.22,3.77,3.23,2.60,1.86,1.03,0.09]
t=[0.00,0.10,0.20,0.30,0.40,0.50,0.60,0.70,0.80,0.90,1.00]
v_x,v_y,temps_v=calcul_vitesses(x,z,t)
representation_vecteur_vitesse(x,z,v_x,v_y)
plt.show()